SP7: Unit Q Concept 2

“Please see my SP7, made in collaboration with Jesus Huerta, by visiting their blog here.  Also be sure to check out the other awesome posts on their blog,”

 

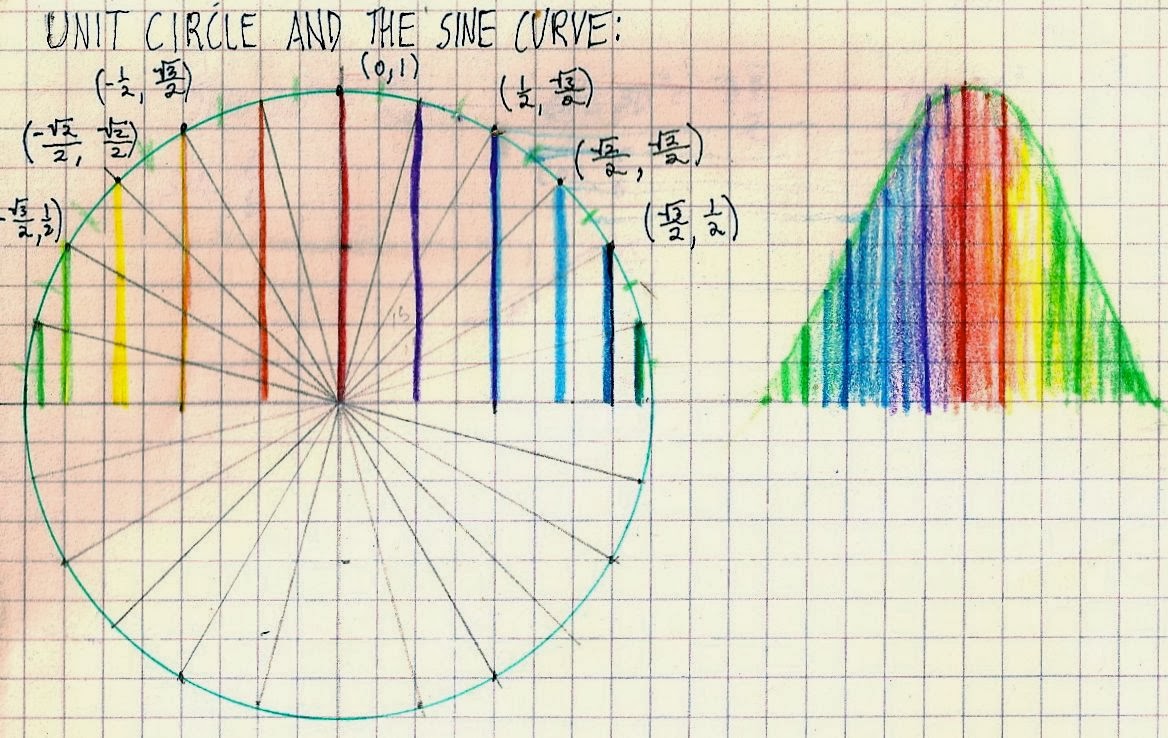
I/D3: Unit Q - Pythagorean Identities

INQUIRY ACTIVITY SUMMARY

1. Where does where sin2x+cos2x=1 come from to begin with (think Unit Circle!). You should be referring to Unit Circle ratios and the Pythagorean Theorem in your explanation.

A: Well first we should ask ourselves what is an identity? And why the Pythagorean Theorem is also an "identity"? An identity are proven facts and formulas that are always true. Then, we should ask ourselves what is the Pythagorean Theorem using x, y, and r? Well it's x^2+y^2=r^2 divided by r^2, which then makes the operation equal to 1. Remember what the ratios are for cosines and sines are in the unit circle. Cosine is (x/r) and Sine is (y/r) and you're able to see that cos^2ø+sin^2ø=1. It's referred to an identity because it's a formula that's always true. For example, (√3/2,1/2) cos30º = (√3/2)^2 = 3/4 and sin30º= (1/2)^2 = 1/4. Cos^2ø+Sin^2ø=1. 

2. Show and explain how to derive the two remaining Pythagorean Identities from sin2x+cos2x=1.  Be sure to show step by step.

A: So first off with we know that sin^2x +cos^2x=1, then you have to divide cos^2x to both sides and that gets you tan^2x+1=sec^2x. And then for the other one we know that sin^2x +cos^2x=1 and now all we have to do is divide sin^2x and we get csc^2x.

INQUIRY ACTIVITY REFLECTION

“The connections that I see between Units N, O, P, and Q so far are…” is that the problems that we work with happen to be similar. For example, the Pythagorean theorem somehow always manages to come out. 

“If I had to describe trigonometry in THREE words, they would be…” awe-struck, mind-blowing, and fun.

WPP #13 & 14: Unit P Concept 6 & 7

“This WPP13-14 was made in collaboration with Rodolfo Rodriguez. Please visit the other awesome posts on their blog by going here

Create your own Playlist on LessonPaths!

BQ# 1: Unit P Concept P: Law of Sines, Law of Cosines, Area formulas

BQ #1: Unit P Concept 1-5: Law of Sines, Law of Cosines, Area formulas

3. Law of Cosines - Why do we need it? How is it derived from what we already know?  

(http://mathworld.wolfram.com/LawofCosines.html)

Answer: The Law of Cosines is a very helpful law that helps us find answers to the triangle we're working on. The Law of Cosines can be used in any triangle. The formula for the Law of Cosines is    but the law itself can be arranged in two other ways. The Law of Cosines is useful for finding: The third side of a triangle when you know two sides and the angle between them. The angles of a triangle when you know all three sides. Also, you can rewrite the c² = a² + b² - 2ab cos(C) formula into "a²=" and "b²=" form.

4. Area formulas - How is the “area of an oblique” triangle derived?  How does it relate to the area formula that you are familiar with?

Answer: What if you wanted to find out the area of the triangle on your left, but did not know the value of h? Could we do it? So, the area of a triangle is A=1/2bh, where b is the base and h is the perpendicular height of the triangle. In the given triangle on the left, we know that sinC= h/a, and therefore h=asicC. Substituting in our regular area equation for h, we get A=1/2b(asinC). The area of an oblique (all sides different lengths!) triangle is one-half of the product of two sides and the sine of their included angle (the angle in between them). Depending on which sides and angles we know, the formula can be written in three ways:

Either: Area = 1 ab sin C 2

Or: Area = 1 bc sin A 2

Or: Area = 1 ca sin B 2

There are different ways to find an area of a triangle. You can calculate the area of a triangle if you know the lengths of all three sides, using a formula that has been know for nearly 2000 years. :O 
References/Citations:
http://www.mathsisfun.com/algebra/trig-cosine-law.html
http://mathworld.wolfram.com/LawofCosines.html
http://www.mathsisfun.com/geometry/herons-formula.html
http://www.mathsisfun.com/algebra/trig-area-triangle-without-right-angle.html

I/D# 1: Unit N Concept 7

INQUIRY ACTIVITY SUMMARY

(http://www.wyzant.com/resources/lessons/math/trigonometry/unit-circle)

1. Describe the 30* triangle

The 30 degree triangle is one of the triangle that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 30 degree triangle has several things to it, which are the sides when you use sohcahtoa, or in other words sine, cosine, and tangent. The angle itself is already given. The triangle itself also happens to land on the first (I) quadrant and everything in the first quadrant have positive angles and coordinate points. Another interesting fact about the unit circle is that when we want to find the radians for the 30 degree triangle all we have to do is multiply 30* times Pi and divide it by 180, which then gets you pi/6. To get Rad 3 / 2 and 1/2 is that you have to take in consideration that there's a chart that'll be on your bottom explaining to you why those are the numbers you want to have instead of some other numbers.

(http://www.mathsisfun.com/geometry/unit-circle.html)

2. Describe the 45* triangle

The 45 degree triangle is one of the other triangles that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 45 degree triangles also has several things to it, which are the sides you use sohcahtoa, or in other words sine, cosine, and tangent. Just like the 30 degree triangle the 45 degree angle itself is already given. Just like the 30 degree triangle the 45 degree also happens to land on the first quadrant and everything that you work around with it is positive. Another interesting fact about the unit circle is that when we want to find the radians for the 45 degree triangle all we have to do is multiply 45* times Pi and divide it by 180, which then gets you pi/4. To get the Rad 2/2 and rad 2/2 is that you have to take in consideration that there's a chart that'll be on your bottom explaining to you why those are the numbers you want to have instead of some other numbers.

(http://www.wyzant.com/resources/lessons/math/trigonometry/unit-circle)

3. Describe the 60* triangle

The 60 degree triangle is one of the other triangles that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 60 degree triangle also have different things to it , which are the sides when you use sohcahtoa, or in other words sine, cosine, and tangent. Just like the two above 30 degree and 45 degree angle triangles, the 60 degree (angle) has already been given. Just like the 30 degree and 45 degree angle(s), the 60 degree angle also lies on the first quadrant and everything that you work around with it is positive. Another interesting fact about the unit circle is that when we want to find the radians for the 60 degree triangle all we have to do is multiply 60* times Pi and divide it by 180, which then gets you pi/3. To get 1/2 and Rad 3/2 is that you have to take in consideration that there's a chart that'll be on your left also explaining to you why those are the numbers you want to have instead of some other number.

4. How does this activity help you to derive the Unit Circle? This activity helps me derive the Unit Circle in so many ways that I wish I could just show all of the upcoming sophomores who are about to take Math Analysis Honors next year. But mathematically speaking the Unit Circle helps you out a lot when it comes to the tests because if you don't know what something is right away when you're doing a problem and you have to refer back to the Unit Circle like everything is all there. Jesus is there with you no lie. But if you had to memorize the Unit Circle it would be somewhat difficult because you don't know what it would mean or where it came from but since we have an excellent math teacher then you know exactly why the answers are just like that. Our teacher helps explain the tree map of the Unit Circle like why those numbers are there. She helps us explain the quadrants, functions, ratios, and all of that good stuff. And all of that helps me and benefits me for future classes that I will hopefully take in college. You get the idea on why the Unit Circle is the way it is.

http://www.futurebird.com/wp-content/uploads/qq1.jpg

 5. What quadrant does the triangle drawn in this activity lie in? How do the values change if you draw the triangles in Quadrant II, III, or IV?  Re-draw the three triangles, but this time put one of the triangles in Quadrant II, one in Quadrant III, and one in Quadrant IV.  Label them as you did in the activity and describe the changes that occur.


http://yorkporc.files.wordpress.com/2011/10/image65.png
So, the triangles that you see on your left all have something in similar and those are the sides, angles, radians, and the points. They all play something significant to the making of the unit circle and if you see on the second picture to the left you can see that the lines go down from one point to the other point because those points happen to be the same but different areas in which they lie in, which in the quadrants it would be: ALL, Students, Take, Calculus.

INQUIRY ACTIVITY REFLECTION

1. “The coolest thing I learned from this activity was…” that I found out a lot about the Unit Circle there's so much things that goes along with it and your just like whoa!
2. “This activity will help me in this unit because…” it'll strengthen my knowledge of the unit circle.

WPP #12: Unit O Concept 10- PICTURE

Create your own Playlist on LessonPaths!

I/D# 2: Unit O Concept 7-8

Inquiry Activity Summary

(http://upload.wikimedia.org/wikipedia/commons/6/68/30-60-90.svg)30-60-90º Triangle

1. In this 30-60-90º triangle the ratios that make up this triangle is literally 
1:2:3 that respectively measure 30-60-90º angles in this special right 
triangle. So, in this special right triangle we are given that that this is a 30-
60-90º and so basically what that means is how and why do we get the 
numbers that are on the left of you? Well, segment AD crosses down to segment CB and so what that does is that it creates a right triangle given 
that the angles are 30º, 60º, and 90º. But now how do we find the sides for 
each segment? In order to find √3 we must use the pythagorean theorem, a^2+b^2=c^2, and so what we plug in the pythagorean theorem is(segment DB) (1/2)^2, segment CD & CB were (1/2) so square it and you get 1. Next, we leave b^2 because we don't know what that is *hint hint (check out the pictures). Finally, c^2 means the hypotenuse (segment AB) is 2 because when we multiply "n" by 2 we manage to get the segments as you see on the right. "n" as you see in the 2nd picture is a variable that'll represent different types of problems when being applied to that number.

45-45-90º

2. "In plane geometry, constructing the diagonal of a square results in a triangle whose three angles are in the ratio 1 : 1 : 2, adding up to 180° or π radians. Hence, the angles respectively measure 45° (π/4), 45° (π/4), and 90° (π/2). The sides in this triangle are in the ratio 1 : 1 : √2, which follows immediately from the Pythagorean theorem." - Wikipedia. So first off what we should is cut the square diagonally and label your 45-45-90º since we can assume they are since the numbers are being given to us. To prove that the sides are 1, which also equal to "n" because "n" can be any number and basically it is a variable, we have to use the pythagorean theorem, which then later unlocks the true meaning of the hypotenuse. C=√2 because of the Pythagorean Theorem. The 45-45-90º is an easier triangle to decipher. 

Inquiry Activity Reflection1. “Something I never noticed before about special right triangles is…” that I could apply this to my mathematics test on Friday because the concept is somewhat complex. 2. “Being able to derive these patterns myself aids in my learning because…” I will be able to pass the test this Friday.