INQUIRY ACTIVITY SUMMARY
1. Describe the 30* triangle
The 30 degree triangle is one of the triangle that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 30 degree triangle has several things to it, which are the sides when you use sohcahtoa, or in other words sine, cosine, and tangent. The angle itself is already given. The triangle itself also happens to land on the first (I) quadrant and everything in the first quadrant have positive angles and coordinate points. Another interesting fact about the unit circle is that when we want to find the radians for the 30 degree triangle all we have to do is multiply 30* times Pi and divide it by 180, which then gets you pi/6. To get Rad 3 / 2 and 1/2 is that you have to take in consideration that there's a chart that'll be on your bottom explaining to you why those are the numbers you want to have instead of some other numbers.
2. Describe the 45* triangle
The 45 degree triangle is one of the other triangles that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 45 degree triangles also has several things to it, which are the sides you use sohcahtoa, or in other words sine, cosine, and tangent. Just like the 30 degree triangle the 45 degree angle itself is already given. Just like the 30 degree triangle the 45 degree also happens to land on the first quadrant and everything that you work around with it is positive. Another interesting fact about the unit circle is that when we want to find the radians for the 45 degree triangle all we have to do is multiply 45* times Pi and divide it by 180, which then gets you pi/4. To get the Rad 2/2 and rad 2/2 is that you have to take in consideration that there's a chart that'll be on your bottom explaining to you why those are the numbers you want to have instead of some other numbers.
3. Describe the 60* triangle
The 60 degree triangle is one of the other triangles that is introduced in the Unit Circle and a triangle that we worked on during class. The properties of the 60 degree triangle also have different things to it , which are the sides when you use sohcahtoa, or in other words sine, cosine, and tangent. Just like the two above 30 degree and 45 degree angle triangles, the 60 degree (angle) has already been given. Just like the 30 degree and 45 degree angle(s), the 60 degree angle also lies on the first quadrant and everything that you work around with it is positive. Another interesting fact about the unit circle is that when we want to find the radians for the 60 degree triangle all we have to do is multiply 60* times Pi and divide it by 180, which then gets you pi/3. To get 1/2 and Rad 3/2 is that you have to take in consideration that there's a chart that'll be on your left also explaining to you why those are the numbers you want to have instead of some other number.
4. How does this activity help you to derive the Unit Circle? This activity helps me derive the Unit Circle in so many ways that I wish I could just show all of the upcoming sophomores who are about to take Math Analysis Honors next year. But mathematically speaking the Unit Circle helps you out a lot when it comes to the tests because if you don't know what something is right away when you're doing a problem and you have to refer back to the Unit Circle like everything is all there. Jesus is there with you no lie. But if you had to memorize the Unit Circle it would be somewhat difficult because you don't know what it would mean or where it came from but since we have an excellent math teacher then you know exactly why the answers are just like that. Our teacher helps explain the tree map of the Unit Circle like why those numbers are there. She helps us explain the quadrants, functions, ratios, and all of that good stuff. And all of that helps me and benefits me for future classes that I will hopefully take in college. You get the idea on why the Unit Circle is the way it is.
5. What quadrant does the triangle drawn in this activity lie in? How do the values change if you draw the triangles in Quadrant II, III, or IV? Re-draw the three triangles, but this time put one of the triangles in Quadrant II, one in Quadrant III, and one in Quadrant IV. Label them as you did in the activity and describe the changes that occur.

http://yorkporc.files.wordpress.com/2011/10/image65.png
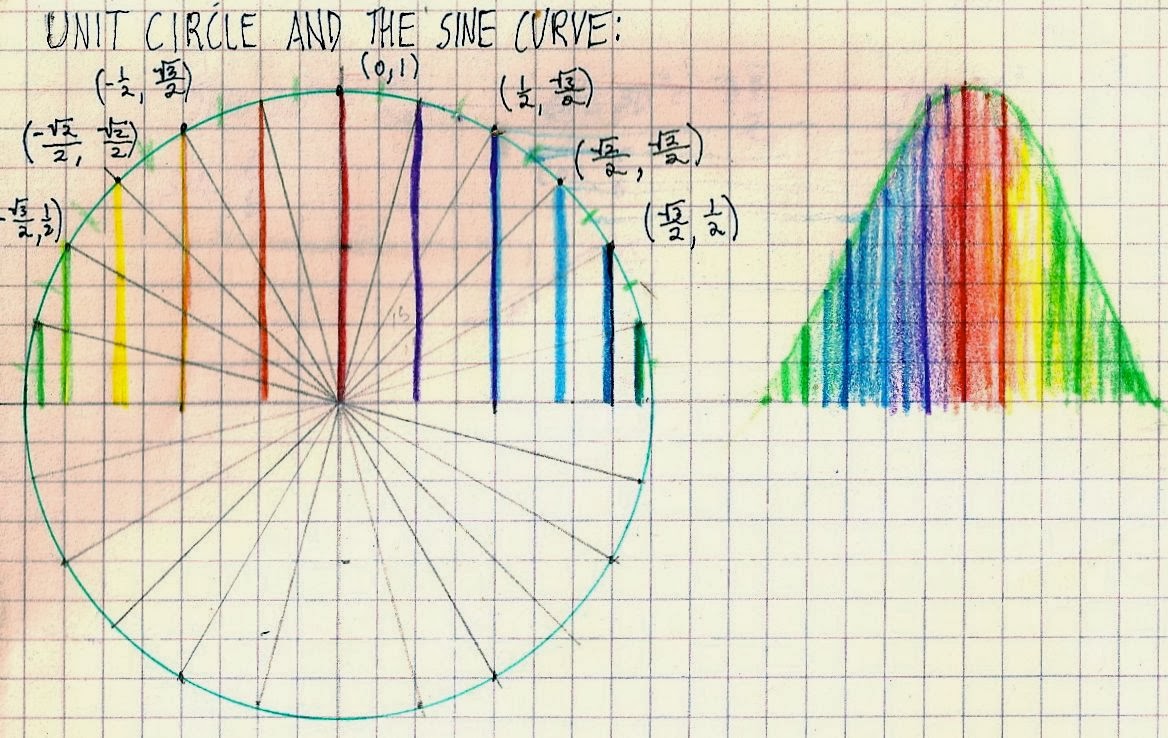
So, the triangles that you see on your left all have something in similar and those are the sides, angles, radians, and the points. They all play something significant to the making of the unit circle and if you see on the second picture to the left you can see that the lines go down from one point to the other point because those points happen to be the same but different areas in which they lie in, which in the quadrants it would be: ALL, Students, Take, Calculus.
4. How does this activity help you to derive the Unit Circle? This activity helps me derive the Unit Circle in so many ways that I wish I could just show all of the upcoming sophomores who are about to take Math Analysis Honors next year. But mathematically speaking the Unit Circle helps you out a lot when it comes to the tests because if you don't know what something is right away when you're doing a problem and you have to refer back to the Unit Circle like everything is all there. Jesus is there with you no lie. But if you had to memorize the Unit Circle it would be somewhat difficult because you don't know what it would mean or where it came from but since we have an excellent math teacher then you know exactly why the answers are just like that. Our teacher helps explain the tree map of the Unit Circle like why those numbers are there. She helps us explain the quadrants, functions, ratios, and all of that good stuff. And all of that helps me and benefits me for future classes that I will hopefully take in college. You get the idea on why the Unit Circle is the way it is.
5. What quadrant does the triangle drawn in this activity lie in? How do the values change if you draw the triangles in Quadrant II, III, or IV? Re-draw the three triangles, but this time put one of the triangles in Quadrant II, one in Quadrant III, and one in Quadrant IV. Label them as you did in the activity and describe the changes that occur.

http://yorkporc.files.wordpress.com/2011/10/image65.png
So, the triangles that you see on your left all have something in similar and those are the sides, angles, radians, and the points. They all play something significant to the making of the unit circle and if you see on the second picture to the left you can see that the lines go down from one point to the other point because those points happen to be the same but different areas in which they lie in, which in the quadrants it would be: ALL, Students, Take, Calculus.
INQUIRY ACTIVITY REFLECTION
- “The coolest thing I learned from this activity was…” that I found out a lot about the Unit Circle there's so much things that goes along with it and your just like whoa!
- “This activity will help me in this unit because…” it'll strengthen my knowledge of the unit circle.




No comments:
Post a Comment